Introducción a la geometría (recta, segmento, semirrecta y rayo)
Comenzaremos mencionando los términos no definidos que son: punto, recta y plano. Los cuales aceptaremos sin definición previa dado que no existe alguna. Las ideas punto, recta y plano estas sugeridas por objetos reales.
Indice de Contenido
Introducción
La palabra Geometría proviene del griego geō, 'tierra'; metrein, 'medir', y es una rama de las matemáticas que se ocupa de las propiedades del espacio. En su forma más elemental, la geometría se preocupa de problemas métricos como el cálculo del área y diámetro de figuras planas y de la superficie y volumen de cuerpos sólidos. Otros campos de la geometría son la geometría analítica, geometría descriptiva, topología, geometría de espacios con cuatro o más dimensiones, geometría fractal, y geometría no euclídea.

El Punto
Si se hace una marca en una hoja de papel con la punta de un lápiz, se obtiene una representación bastante fiel de un punto, la representación será mejor, cuando más afilado sea el lápiz. El dibujo siempre será próximo, pues la marca tendrá alguna área, mientras que el punto carece de área.
Pero si se piensa en marcas cada vez más pequeñas, hechas pro lápices cada vez más afilados, se obtendrá una buena idea del término punto. Para representar un punto utilizaremos letras mayúsculas y los leeremos: punta A, Punto B, Punto C. etc. El punto es uno de los entes fundamentales, junto con la recta y el plano. Son considerados conceptos primarios, es decir, que sólo es posible describirlos en relación con otros elementos similares o parecidos.
Ejemplos de puntos en la figura 1


Recta
Es una línea infinita que describe de forma idealizada la imagen real de un hilo tenso o de un rayo de luz. La recta, al igual que el punto o el plano, es un concepto primitivo, que no se puede definir si no es recurriendo a otros conceptos que, a su vez, para ser definidos requieren de la recta. Cuando empleamos la palabra recta, tenemos siempre en la mente la idea de una línea recta, una recta de extiende indefinidamente en ambos lados, por lo regular indicamos estos en las ilustraciones, marcando flechas en los extremos de las porciones de rectas que dibujamos así: ver la figura 2
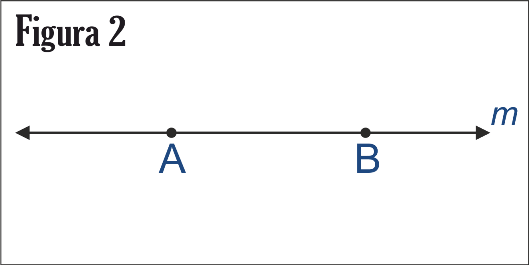

Las puntas de la flecha servirán para recordarnos que la recta no termina en los puntos donde finaliza el dibujo. A menudo se designa una recta por una letra minúscula, como la recta m en la figura 2, simbólicamente también representamos una recta por las letras asignadas a dos puntos cualesquiera de sus puntos y escribiendo una recta pequeña sobre dichos puntos. Quedando como la figura 3


Plano
Es una superficie infinita que describe de forma idealizada la imagen real de la superficie de una mesa o de un lago en calma. El plano, al igual que el punto o la recta, es un concepto primitivo que no se puede definir si no es recurriendo a otros conceptos que, a su vez, para ser definidos requieren del plano.
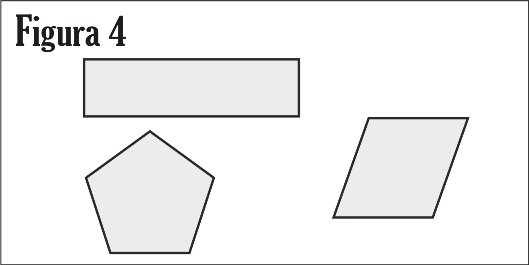
Formas superficiales en dos dimensiones sugieren la idea de un plano, pero dichos objetos solamente son modelos físicos de planos. No son planos; un plano es una abstracción matemática, también podemos pensar en una superficie perfectamente lisa que se extiende indefinidamente en todas las direcciones. Ver figura 4

Segmento
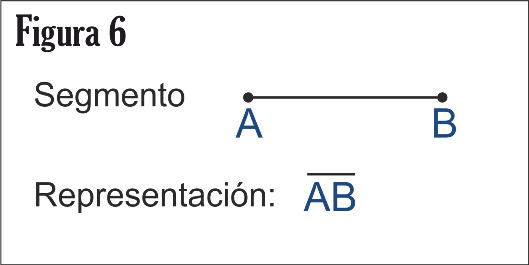
Estudiaremos ahora algunos subconjuntos de la recta que son muy importantes en geometría, en la figura 5, tenemos dos puntos A y B, que pertenecen a la recta l, los puntos A y B determinan lo que se llama un segmento de recta. Segmento rectilíneo o simplemente segmento, es la porción de recta comprendida entre dos de sus puntos que se llaman extremos, o bien uno origen y otro extremo. Los extremos de un segmento forman parte del mismo. Un segmento de extremos A y B se designa AB, y su longitud
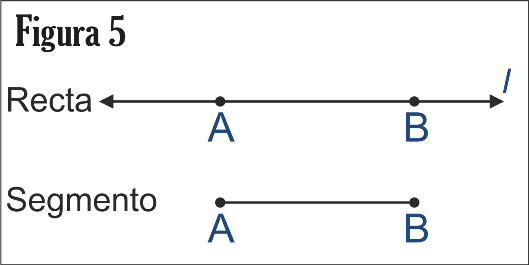

Para los puntos A y B de la recta l en la figura 5 representan un segmento y simbólicamente se representas así: ver figura 6

Semirrecta
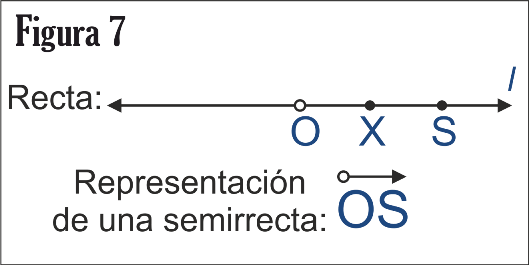
En la figura 7 el punto O de la recta l separa todos los otros puntos de la recta en dos conjuntos. El punto O no pertenece a ninguno de los conjuntos de puntos de su izquierda ni de su derecha, es un punto abierto solo señalado. A este se llama semirrecta. entonces podemos decir que una Semirrecta, es cada una de las dos partes en que una recta queda dividida por uno de sus puntos, al que se llama origen.

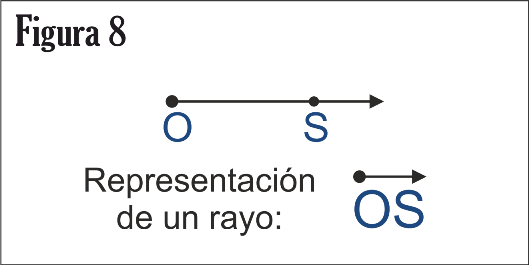
Rayo
La unión del punto que contiene al punto O y a una semirrecta se llama rayo y el punto O se llama extremo del rayo ver figura 8.