Intervalos (Acotados y no Acotados)

Es un espacio métrico comprendido entre dos valores a y b y que son representados en una recta numérica, que dependiendo sus extremos estos se dividen en intervalos acotados y los intervalos no acotados. Los intervalos se determinan sobre la recta real y, por tanto, se corresponden con conjuntos de números. Pueden ser abiertos, cerrados o semiabiertos.

Introducción

En matemáticas, un intervalo es un conjunto de números reales que se extiende entre dos valores. Formalmente, dado dos números reales a yb con a<b, el intervalo se denota como [a,b] y se define como el conjunto de todos los números reales x tal que a≤x≤b. Esto implica que el intervalo contiene tanto el límite inferior a como el límite superior b, junto con todos los números reales en el intervalo.

Los intervalos se utilizan para determinar los dominios y rangos de las funciones. En el Cálculo, Son fundamentales para definir los intervalos de convergencia en series y sucesiones, además en geometría analítica, los intervalos son esenciales para definir los intervalos en los que se encuentran las coordenadas de un punto.

Los intervalos acotados

Son los intervalos cuyos extremos se encuentra en una serie de combinación entre abiertos y cerrados pero con un final marcado entre los dos puntos a y b, estos a su vez se dividen en: intervalos acotados cerrados, intervalos acotados abiertos y en intervalos acotados semi abiertos o semi cerrados.

 

Los intervalos no acotados

son intervalos cuyo principio está bien marcado pero el extremo final siempre estará al infinito ya sea negativo o positivo, estos a su vez se dividen en: intervalo no acotado cerrado en A hacia el infinito positivo, intervalo no acotado abierto en A hacia el infinito positivo, intervalo no acotado cerrado en A hacia el infinito negativo y el intervalo no acotado abierto en A hacia el infinito negativo.

 

Escritura para intervalos: El número menor siempre se escribe a la izquierda del mayor, utilizamos corchetes para afuera ( ] [ ) cuando un extremo no está incluido en el intervalo, usaremos corchetes hacia adentro ( [ ] ) cuantos un extremo este incluido, notemos que cuando un intervalo este al infinito ese extremo siempre estar con corchete abierto. 

Tabla para los intervalos acotados

   

 

Tabla para los intervalos No acotados

 

 

Ejercicios

Conclusiones

Los intervalos se determinan sobre la recta real y, por tanto, se corresponden con conjuntos de números. Pueden ser abiertos, cerrados o semiabiertos.

Un intervalo cerrado es un segmento, AB, en el que se incluyen los extremos. Si las abscisas de los puntos A y B son respectivamente a y b, el intervalo cerrado se designa [a, b] y representa al conjunto de todos los números reales comprendidos entre a y b, incluyendo los extremos: [a, b] = {x / a ≤ x ≤ b}

Un intervalo abierto de extremos a y b se designa (a, b) y representa al conjunto de los números reales comprendidos entre a y b, es decir, mayores que a pero menores que b: (a, b) = {x / a < x < b}

Un intervalo semiabierto de extremos a y b puede ser (a, b] o [a, b):

(a, b] = {x / a < x ≤ b} (se excluye a y se incluye b)

[a, b) = {x / a ≤ x < b} (se incluye a y se excluye b)

En una concepción más amplia, también se denominan intervalos los conjuntos infinitos con un único extremo (semirrectas):

(-∞, b] = {x / x ≤ b}. Es el conjunto formado por el número b y todos los números reales menores que b.

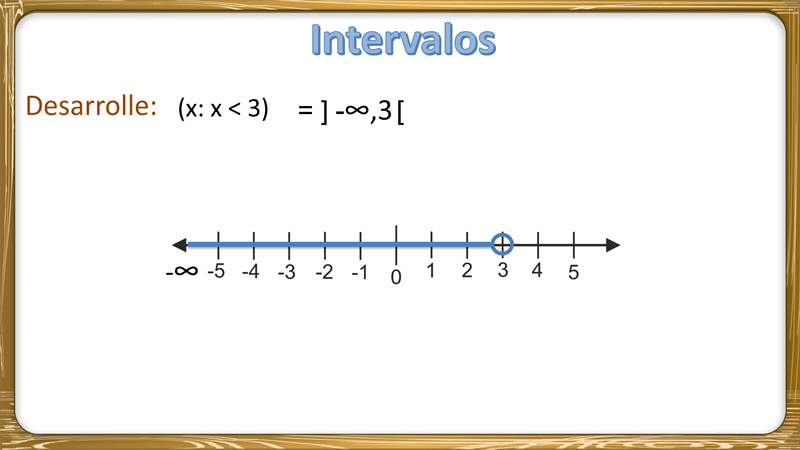
(-∞, b) = {x / x < b}. Es el conjunto formado por todos los números reales menores que b.

(a, ∞) = {x / x > a}. Es el conjunto de todos los números reales mayores que a.

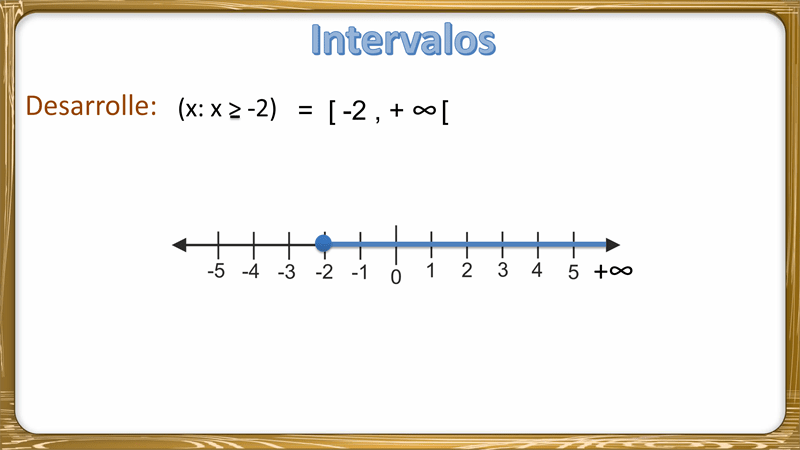
[a, ∞) = {x / x ≥ a}. Es el conjunto formado por el número a y todos los números reales mayores que él.

La nomenclatura utilizada para la designación de intervalos es, en resumen, la siguiente:

► Para incluir los extremos se utilizan los corchetes: ], [ 

► Para excluir los extremos, los paréntesis: ), ( 

► Para alejarse indefinidamente a la derecha, el signo ∞ cerrado con un paréntesis: (3, ∞) números mayores que 3. 

► Para alejarse indefinidamente a la izquierda, el signo -∞ abierto con un paréntesis: (-∞, 3) números menores que 3.