Número decimal: ¿Qué son y como se usan?

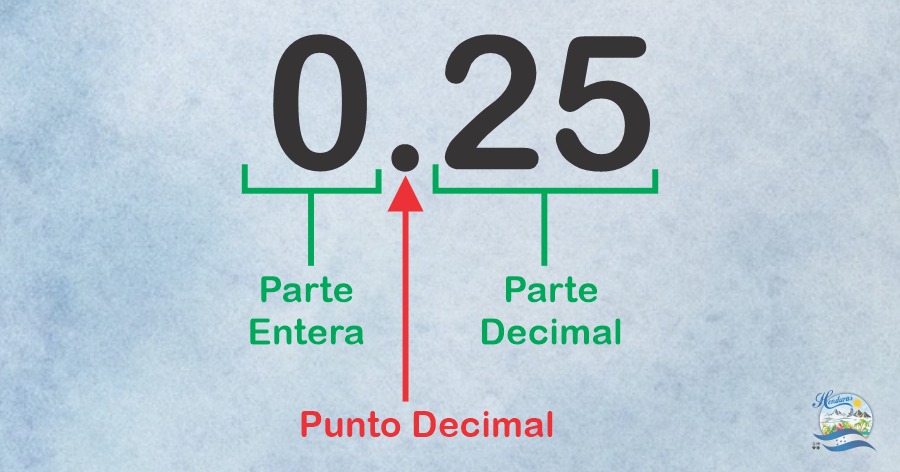
Un número decimal consiste en una parte entera y una fracción decimal. Habitualmente, se reconoce un número decimal como aquel representado utilizando el sistema de numeración decimal, colocando primero una parte entera, seguido de un punto decimal, y finalizando con la parte decimal, (ejemplo = 0.25).

Introducción

En algunos contextos, un número decimal se define formalmente como un número que puede expresarse como el cociente de un número entero y una potencia positiva de 10, conocido también como fracción decimal. Según esta definición, si se consideran solo los cocientes exactos, los números decimales son aquellos con una cantidad finita de cifras en su parte decimal, es decir, se trata de números decimales finitos o exactos.

Sin embargo, en otras regiones y contextos, esta definición formal no se aplica exclusivamente a los números decimales, sino a las fracciones decimales. En estos casos, un número decimal se considera simplemente como un número que incluye una parte entera y una parte fraccionaria. Así, no se excluyen representaciones decimales infinitas de otros números reales, incluidos los irracionales como el número π (pi). Este tema ha generado debates entre académicos e investigadores en el campo de la didáctica de las matemáticas sobre cómo presentar y enseñar los números decimales.

Notación decimal

En el español actual, existen tres métodos principales para anotar números con decimales, dependiendo del signo utilizado como separador decimal:

1. Punto decimal: Se utiliza un punto (.) para separar la parte entera de la parte decimal. Este método es común en calculadoras electrónicas y computadoras, así como en países como México, aunque es menos frecuente en otros países hispanohablantes cuando se escriben cifras manualmente:

Ejemplo: 3.141592

2. Coma decimal: Se emplea una coma (,) para dividir la parte entera de la decimal. Esta forma es común en publicaciones en español (excepto en México) y también se usa en notaciones manuales:

Ejemplo: 3,141592

3. Apóstrofo decimal: Se usa un apóstrofo (') para separar la parte decimal de un número en notaciones manuscritas; sin embargo, esta forma es considerada incorrecta según la Real Academia Española (RAE):

Ejemplo: 3'141592

En todos los casos, las cifras decimales se escriben juntas, sin espacios u otros signos que las separen, independientemente de la cantidad de cifras decimales que tenga el número.

Clasificación

Siguiendo esta definición, donde la parte entera es la que se encuentra a la izquierda del separador decimal y la parte decimal es la que se encuentra a la derecha, se puede establecer la siguiente clasificación:

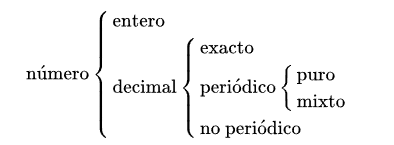
Número decimal exacto

Los números decimales exactos son aquellos cuya parte decimal tiene un número finito de cifras. Estos números pueden expresarse como fracciones, lo que los clasifica dentro del conjunto de los números racionales.

1/5 = 0.2

Una característica notable de estos números es que su representación decimal no es única. Por ejemplo, el número racional 1/5 ​ puede representarse como el número decimal exacto 0,2.

Número decimal periódico

Los números decimales periódicos son aquellos cuya parte decimal tiene un número infinito de cifras que se repiten siguiendo un patrón regular, conocido como periodo. Si el patrón de repetición empieza inmediatamente después del separador decimal, se denominan números decimales periódicos puros. Si el patrón de repetición empieza después de una serie de cifras no repetitivas, conocida como anteperiodo, se llaman números decimales periódicos mixtos.

Estos números forman parte del conjunto de los números racionales, ya que pueden expresarse en forma de fracción.

Decimal periódico puro

Los números decimales periódicos puros son aquellos en los que la parte decimal repite un patrón de cifras inmediatamente después del separador decimal. Esta parte repetitiva, conocida como el periodo, se suele indicar con una línea horizontal superior sobre las cifras que se repiten.

0.3 = 0,3333...

Decimal periódico mixto

Los números decimales periódicos mixtos son aquellos en los que la parte decimal consta de una parte no repetitiva, llamada anteperiodo, seguida de una parte que se repite indefinidamente, conocida como periodo. La parte periódica se indica comúnmente con una línea horizontal sobre las cifras que se repiten.

0.16666666

Al igual que los números decimales periódicos puros, los números decimales mixtos siempre pueden ser expresados en forma de fracción. Por ejemplo, el número decimal 0.16 (donde "16" es el periodo) se puede representar como la fracción 1/16, Esta propiedad confirma que los números decimales periódicos, ya sean puros o mixtos, pertenecen al conjunto de los números racionales, que son aquellos que pueden expresarse como el cociente de dos números enteros.

Número decimal no periódico

Los números decimales no periódicos tienen una parte decimal infinita que no se repite en ningún patrón regular. Estos números pertenecen al conjunto de los números irracionales, los cuales no pueden ser expresados como el cociente de dos números enteros, es decir, no pueden ser representados mediante una fracción.

π (pi) = 3,141592…

Ejemplos típicos de números irracionales incluyen π (pi) y raíz cuadrada de 2​, cuyas expansiones decimales no tienen un patrón repetitivo y se extienden infinitamente.